Hunter-Runner

Hunter-Runner: Implementing HIVEMind on FlexBot

The Search Algorithm

We conceive of the map as a standard graph representation with nodes (waypoints) and edges (connections between the waypoints). Waypoints are always line-of-sight. The Runner and Hunters know their starting locations, as well as the exit points. When the Hunters start, their first priority is to travel to the exit points in order to prevent the Runner from reaching its goal. There is at least one Hunter per exit point. If there are more Hunters than exit points, the leftover Hunters will arbitrarily pick an exit point. 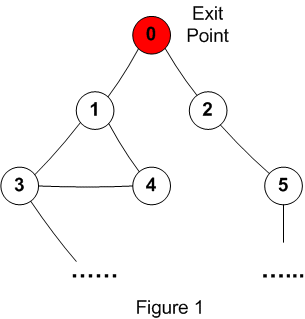When the Hunters arrive at the exit point, we can now view the graph with the exit points as the root nodes. Figure 1 below shows a simple map with one exit point at node 0.

Now, the algorithm proceeds in the following way:

For the next level in the graph, figure out how many corridors are there connected to nodes on the current level. Right now, all the Hunters are currently located at node 0, and there are two corridors leading out from node 0. Therefore, node 0 requires at least two Hunters to start.
If the total number of required Hunters is not enough (2 in this case), then we should just halt here. We can't actively search the rest of the map without exposing some path to the exit.
If we have enough Hunters, then move the Hunters into the appropriate starting positions. Begin traversing the corridors after all the Hunters have moved into the appropriate starting positions. So, one Hunter traverses 0->1, and the remaining Hunters traverse 0->2.

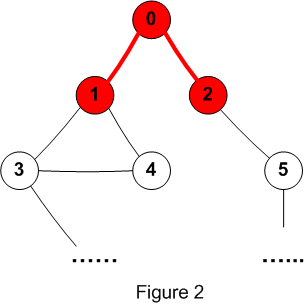When all the Hunters have arrived at either nodes 1 or 2, the algorithm simply repeats:

Node 1 has two corridors extending from it, and node 2 has one. So we need at least three Hunters total to search the next level of the graph.
If we don't have enough enough Hunters, we should stop moving forward. We can't trap the Runner, but at least we can prevent her from reaching the exit.
If we have enough Hunters, then move two to node 1, and the rest to node 2. After they arrive, traverse corridors 1->3, 1->4 and 2->5.

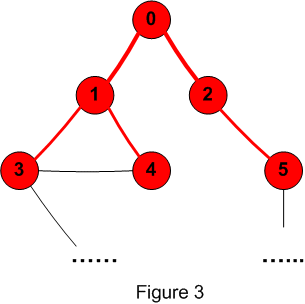Again, we keep repeating the algorithm until all corridors have been searched, or the Runner is found and trapped. The Runner can either be trapped in a dead end, or in a corridor between two Hunters.

Obviously, this algorithm is suboptimal. So we have a priori knowledge of the map, we can actually pre-calculate an optimal search path through the graph given the available number of Hunters. At present, time is wasted maneuvering the Hunters into their initial positions before they traverse the corridors.

However, the point of this experiment is not to find an optimal search path through the graph. Rather, it is to show the power of the communication architecture we have utilized for this task. Furthermore, our communication architecture supports the ability to dynamically add or subtract team members during run-time. So the a priori calculation based on the starting number of bots could be invalidated if the size of the team changes during run-time.

<<<<< The Hunters | The HIVEMind >>>>>

khoo@cs.northwestern.edu