Project 2
CS351: Introduction to Computer Graphics
Due 11:59pm, Friday, October 15th



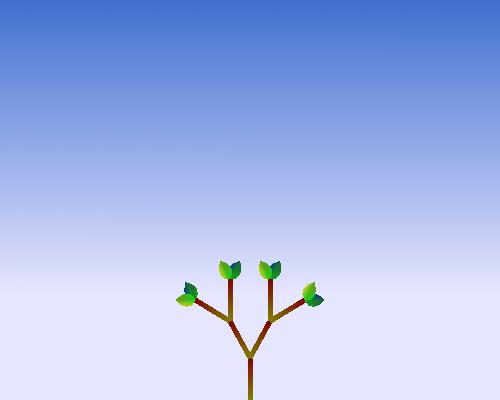
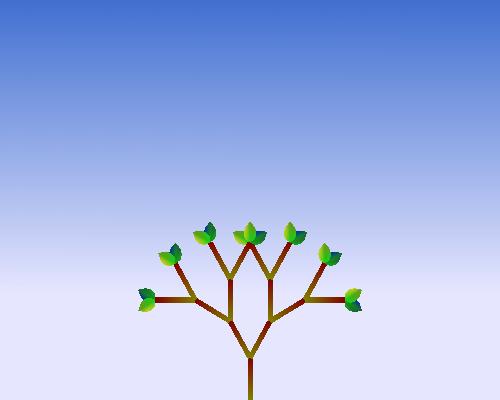
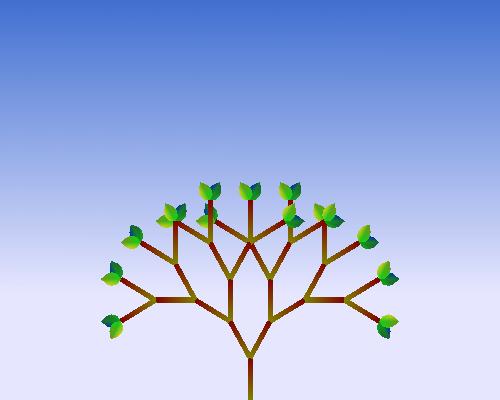
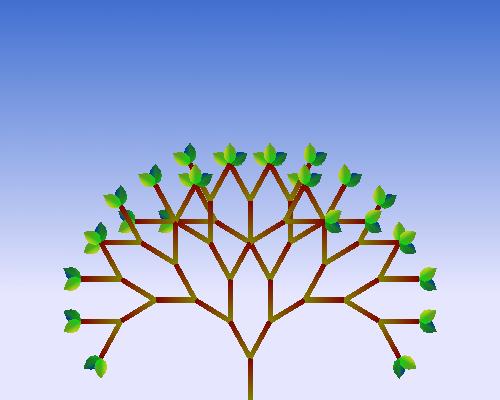
Due 11:59pm, Friday, October 15th








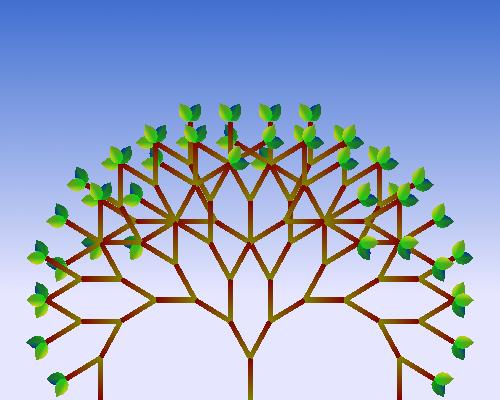
In this project we will draw two-dimensional fractal plants. Part of the project is implementing and using your own transformation matrices; this is so that you'll understand how they are used in OpenGL and other graphics systems. I will give you a template with which you will need to modify. The basic project described below is worth 100 points. To do A-level work, you'll need to implement some additional features.
You may use any of the OpenGL functions for drawing primitives: glBegin(GL_POLYGON), glBegin(GL_TRIANGLES), etc., and you can set colors using glColor3f.
You must specify the transformations used by your L-system by specifying your own matrices, and loading them into the OpenGL MODELVIEW matrix. (You may not use stl or any other matrix library). By loading your matrix into the MODELVIEW matrix, you allow OpenGL to use it to produce the correct world coordinates for each vertex. The OpenGL commands you may NOT use this time are glRotate, glScale, glTranslate, glMultMatrix, glPushMatrix and glPopMatrix - they are OpenGL's version of the matrix modification functions. Instead, you should keep track of your own 2D version of the MODELVIEW matrix, and modify it by post-multiplying it by translation matrices, rotation matrices, etc. I think it is far easier to write a 4x4 matrix class, similar to what OpenGL uses (ie an array such as: GLfloat myMat[16]), as discussed in class.
The base code program should make use of the recursion depth of the L-system specified by the variable "ITER", which can be increased or decreased with the keyboard. Please do not change the mapping of the keyboard it will make it easier for me to grade. (you may however change the variable name.
For example,
ITER = 5
should draw the plant corresponding to 5 iterations
of your L-system.
Check out these ideas for improvments you can make to the project. Anything else that I think is interesting and/or neat looking might get extra credit, so don't feel constrained by this list. If you have a good idea, go for it! If you're wondering if it's a good idea, ask.
You can either download proj2.tar.gz or grab each of the files below:
Optional helpful files:
Look here for some advice about getting started.
Please take a picture of your best plant, suitable for framing or for display on the class Web page, and save it as a either a tif, a jpg, or a gif.
On the some machines you can do this using the grab function of xv. Type xv to get started.
You can also use the information on the class web page to be able to save out tif's from your OpenGL program.
Thanks!