Planning is one of the classic problems of Artificial Intelligence. Here we just touch on the most basic concepts in the simplest way, and show how planning can be approached using a deductive reasoner.
The Planning Problem
Here's a simplified statement of the planning problem.
- You have a current state of the world.
- You have a desired state of the world.
- Find a sequence of actions that, if executed, should change the world from its current state into the desired state.
A planner is a program that can solve planning problems.
Military planning is an obvious, and long-studied, example of planning. It's particularly challenging because it mixes not only planning, which is hard enough, but game playing against an uncontrollable opponent.
To keep things simple, early work in AI focused on planning where no opponent is involved, the world is fairly simple, and things don't change unless the actor, e.g., a robot, causes them to change when executing the plan. We'll make those assumptions here.
In real planning research, the goal is to find very general rules for selecting steps that can be used in every problem. These rules look at the states and the plan so far. We will have a general planner, but very specific rules for each problem.
Deductive Rules for Planning
Using just our simple backward chainer, we can define a general
planning framework, that involves a few basic concepts, and two
core deductive rules.
We start with the predicate PLAN.
(PLAN steps start goal)
This should be true if doing
the steps listed would transform an initial
situation start into a desired situation goal.
We'll represent the list of steps with
CONS and NIL. That means we can use rules
for predicates
like APPEND and MEMBER in our planning rules.
How we represent individual steps and states will depend on the specific
problem domain.
PLAN.
The first rule is trivial.
(<- (plan nil ?goal ?goal))
This says the empty plan works if the current state is the desired state.
The second rule does all the work. When the start state is not the goal state, the rule looks for actions that will change the state of the world from the current state to the desired state.
(<- (plan (cons ?action ?actions) ?current ?goal)
(not (same ?current ?goal))
(step ?action ?current ?goal)
(results ?action ?current ?result)
(plan ?actions ?result ?goal))
(<- (same ?x ?x))
Here is what the rule says, line by line:
(<- (plan (cons ?action ?actions) ?current ?goal)
?action followed by
?actions will get from
?current to ?goal, if...
(not (same ?current ?goal))
(step ?action ?current ?goal)
?action is a valid step to try given the
current state and the goal state, and...
(results ?action ?current ?result)
?action> in the current state
is the state ?result , and...
(plan ?actions ?result ?goal))
?actions> are a valid plan to
get to the goal state from the result state.
This formulation defines how plans work in general. All the details
about how to represent states, how to represent actions, how actions
affect states, and how to pick valid actions, are
in the rules we define for the predicates STEP and
RESULTS.
Examples
The following two examples are classic early toy examples in AI planning. Cordell Green demonstrated how deductive retrieval could solve such problems in his technical report Application of Theorem Proving to Problem Solving. The planning problem turned out to be a much harder than first realized, and much logical study resulted.
The Blocks World Stacking Problem
At MIT, a lot of early work used the blocks world domain as a testbed for planning ideas. In the blocks world, a robot with a camera and one arm with a grasper is given the task of stacking blocks on a table in some specified arrangement. Since the robot can only move one block at a time, and blocks may already be in stacks, the problem is one of unstacking and stacking. Ideally the planner should create efficient plans with no wasted moves.
We'll make this problem as simple as possible. The robot has just
one stack of blocks to worry about.
We'll represent the state of the world as just a stack of blocks, such as
(CONS A (CONS B (CONS C NIL))) for the stack with
A on B on C.
The task to create a stack can be represented as a query with a variable for the desired plan, the initial stack, and the goal stack. For example, given this problem to solve
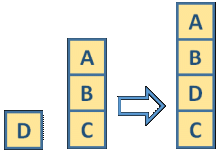
becomes this query:
(plan ?plan (cons a (cons b (cons c nil)))
(cons a (cons b (cons d (cons c nil)))))
Two actions are sufficient for this simple version of the problem:
- the action
POPremoves the block on the top of the stack and puts it on the table - the action
(PUSH x)takes the block x from the table and puts it on the top of the stack
These RESULT rules describe those effects:
(<- (results pop (cons ?x ?stack) ?stack)) (<- (results (push ?x) ?stack (cons ?x ?stack)))
Neither rule needs antecedents in this simple world.
The POP can be applied to any stack with an element on top.
The result state is the stack without that element.
PUSH says that if ?x is put on the stack, then
it appears on top in the result state.
Note that these rules are not changing any data structures. They are just rules about how this "world" works, how things would change if actions were taken in a given world state.
The harder part is writing STEP rules to say when to POP
or PUSH. It would be easy to get into an endless loop here. A deductive
planner tries all possibilities. We don't want our planner to say "what if I
PUSH A and then POP and then PUSH A
then POP then ..." We have to write rules
for STEP that direct the planner "toward" the goal in some way that
doesn't lead to cycles.
At this point, it pays to do a number of examples by hand, from one or two blocks to
three or four, in different arrangements, to get a feeling for when to POP and
when to PUSH. Eventually, the following rules for selecting
when to POP and PUSH should make sense:
- Pop until the current stack matches the bottom of the goal stack
- Push a block X if X + the current stack matches the bottom of the stack
In the example problem given above, the first rule would pop every block until the stack has just block C. Then the second rule would push D, to make the stack D C, then push B, to make the stack B D C, and then push A, to make the stack A B D C. Only those choices make stacks that incrementally match the bottom of the goal stack.
How do we write a rule to test if the current stack matches the bottom of the goal stack? Since we are using lists to represent stacks, this turns out to be very simple. A stack A matches the bottom of another stack B if there is a list that could be appended to the front of A to make B. So our step selection rules are:
(<- (step pop ?current ?goal)
(not (append ?top ?current ?goal)))
(<- (step (push ?x) ?current ?goal)
(append ?top (cons ?x ?current) ?goal))
Study these for a while. The first rule uses
the NOT logical operator.
For the second rule, ask yourself
"How does it figure out what ?X should be?"
These are the rules, the rules for APPEND,
and the two PLAN rules are
we for the one-stack blocks world planner,
You can try them out by loading
sddr-plan.lisp. You can see some test problems
in
sddr-plan-tests.lisp.
The Monkey and Bananas Problem
While MIT had Blocks World, John McCarthy at Stanford had the Monkey and Bananas problem. A monkey enters a room. Hanging from the ceiling is a bunch of bananas, just out of reach. Over by the window is a box. The planning problem is to generate the plan that gets the bananas by moving the box under the bananas and climbing on top of the box.
The only thing we really care about in this problem are the locations of the monkey, box, and bananas. To make things really simple, we'll put the bananas in the center of the room. So a simple state representation that has only one way to describe any state is
(state monkey-location box-location)
The box can be at the DOOR, WINDOW or CENTER. The Monkey can be those places or BOX-TOP.
If the monkey starts at the door and the box is by the window, then the basic problem query is
(plan ?plan (state door window)
(state box-top center))
I.e., the box has to end up under the bananas and the monkey has to be on the box.
There are three actions the monkey can do. It can walk to a location, push the box to a location, or climb on the box. The action result rules are pretty simple, but unlike the Blocks World, there are some preconditions that have to be true for some actions to be possible. These preconditions are not the same as the step selection rules.
The monkey can climb on the box if the monkey is in the same location as the box.
(<- (results climb-box
(state ?bloc ?bloc)
(state box-top ?bloc)))
Notice how we use repeated variables to require the monkey and box to be in the same location.
The monkey can push the box to a location if the monkey is in the same location as the box. The location of both changes.
(<- (results (push-box ?bloc2)
(state ?bloc1 ?bloc1)
(state ?bloc2 ?bloc2)))
The monkey can walk to any location.
(<- (results (walk-to ?mloc2)
(state ?mloc1 ?bloc)
(state ?mloc2 ?bloc)))
Now we need to guide the monkey to choose actions that lead toward getting the bananas, and never fall into an endless loop.
For example, if the monkey is not where the box is or already on the box, then the monkey should walk to the box.
(<- (step (walk-to ?bloc)
(state ?mloc ?bloc)
(state ?mloc-2 ?gloc))
(not (same ?mloc-1 ?bloc))
(not (same ?mloc-1 box-top)))
Note the use of (not (same ...)). Simply
writing different variables does not ensure different
values.
Similarly, if the box is not where the bananas are -- the goal location -- then the monkey should push the box to that location.
(<- (step (push-box ?gloc)
(state ?bloc ?bloc)
(state ?mloc ?gloc))
(not (same ?bloc ?gloc)))
Finally, if the box and monkey are at the desired location, the monkey should climb on the box.
(<- (step climb-box
(state ?gloc ?gloc)
(state box-top ?gloc)))
These rules, plus the two general PLAN rules,
will solve the problem.
You can try them out by loading
sddr-plan.lisp.