Obsolete
This exercise page has been superseded by this one, using the Simple Deductive Data Retriever. Do not do the exercises listed on this page.
There are two sets of exercises here, using the simple Deductive Data Retriever:
- Solving logical representation problems:
- Overview
- Defining logical rules for list membership
- Defining logical rules for all-different
- Solving the map coloring problem with logic
- Making the Retriever work better:
Using the Deductive Data Retriever
Anyone should be able to work on the logic rule problems. Watch out for infinite loops!
These exercises require the following files from the CS 325 library:
- ddr.lisp -- the code for the Deductive Data Retriever
- ddr-tests.lisp -- the test cases for the Deductive Data Retriever
- ddr-exs-tests.lisp -- the test cases for these exercises
ddr-tests.lisp and ddr-exs-tests.lisp define all their tests in the package named ddr-tests. The easiest way to work on these exercises is to write all your code in the ddr-tests package, that is, create a file and start the file with (in-package #:ddr-tests).
When defining rules, put them in the global variables
listed in the exercise description,
using defparameter. The test cases will automatically load those variables
for you. Send those variable definitions to the Critic when done.
Feel free to create new test cases!.
Exercise: member
Global variable name: *member-kb*
Tests: member in
ddr-exs-tests.lisp
Use defparameter to define *member-kb*
to hold a set of rules to define a deductive (not Lisp!) member
predicate. The query (member x l) should be
true if and only if x is a member of the list l.
Look at the append example
in ddr-tests.lisp
to see how to represent lists with (cons x y)
functional terms.
Exercise: all-different
Global variable name: *all-different-kb*
Tests: all-different in
ddr-exs-tests.lisp
We rarely need an "is equal" predicate with a deductive retriever. For example,
if you want to say some binary relationship always holds for an object
with itself, just say (relation ?x ?x), not (<- (relation ?x ?y)
(equal ?x ?y)).
On the other hand, we do often need an "is different" predicate. For example, in the Monkey and Bananas code in ddr-tests.lisp, we want to the monkey to go to the box only if the monkey's current location is different than the box's location.
To make it easier to assert (different x y),
the code in the Monkey and Bananas formulation
in ddr-tests.lisp defines
a forward-chaining rule so that asserting (different x y)
automatically asserts (different y x). (Why can't this
be a backward-chaining rule?)
That forward-chaining rule cuts the number of assertions needed in half, but we still need to write order(N2) assertions for N objects.
Use defparameter to define *all-different-kb*
to hold a set of rules to define forward-chaining rules for the predicate
(all-different list), where a list is represented
with
(cons x y) functional terms. Asserting
(all-different list) should cause
(different x y) to be asserted for every
pair of different items in the list. Assume there are no duplicates
in the list.
Exercise: Map Coloring
Global variable name: *map-color-kb*
Tests: color-map1, color-map2, and
color-map3in
ddr-exs-tests.lisp
The map coloring problem has a long history. The problem is simple: given a map of various countries bordering each other, color the map using the fewest number of colors, such that no countries sharing a border of more than a point have the same color. For many years, it had been proven that 5 colors was sufficient for any flat map, no matter how complex, and that no map was known that needed more than 4. It finally required a computer to generate the complete proof that 4 was enough.
Here are three small maps, one already colored, the others left for you to figure out:
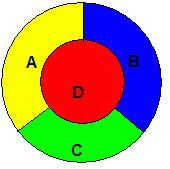
|
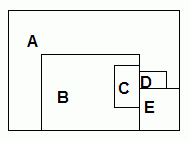
|
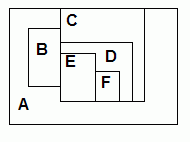
|
Here is a more complicated map that Martin Gardner claimed required 5 colors.
You can encode a map coloring problem in logic with:
- some assertions about what different colors there are, and
- rules (at least one per problem) for a predicate that says whether some map coloring is legal for map; the rules describe the coloring constraints that have to be satisfied.
Define a KB with the colors red, blue, green and yellow.
Then define map coloring rules for the predicate
(colors-for map a-region-color b-region-color c-region-color...),
so that the test cases below pass.
Note that colors-for is given a different
number of arguments for each map. This is not a mistake nor
anything you have to treat specially.
You can have rules for all three maps at the same time. The map
argument will keep the rules separate.
Side question: The above maps all have 24 possible solutions. Do all maps have 24 solutions?
Improving the Deductive Data Retriever
These exercises can make the Retriever less prone to infinite loops, though they may also make it run a bit slower.
Do these as "patch files." That is, don't change the code in ddr.lisp, but create a new file, e.g., ddr-patch.lisp. This file should be in the ddr package and contain only the new and changed definitions necessary to change the Retriever. That way I can see your changes in one place and test them, if necessary, by loading the original ddr.lisp and your patches.
Make sure all the old tests in ddr-tests.lisp continue to work as you modify the retriever, unless the modification makes some test inappropriate.
The email rules still apply. Use the Lisp Critic on your code before sending.
Exercise: assert-file
This one's easy, if you've done the I/O chapter.
Define (assert-file pathname) to assert every fact and/or rule in the file named by pathname. It should return a count of how many items were asserted.
movies.lisp is a very large file of movie facts, adapted from a data file for a Prolog course. Test your code on that. It should say that it loaded 2909 items. Make sure you've compiled ddr.lisp before trying to load this file, otherwise Allegro may never finish!
Exercise: DDR ask-1
The goal of this exercise is to make it possible to get answers one at a time from the Deductive Retriever, somewhat the way the Prolog interpreter works. It should be possible to get one answer and stop, and not pay the cost of looking for other answers. This approach has two advantages. First, if one answer is sufficient, you can get it faster. Second, if a query has an infinite number of answers, a particular application can ask for the first N answers.
This does not prevent infinite loops. If you have rules with that can loop forever, you can still get an infinite loop if you ask something that has no answer.
More specifically, in this exercise you need to
- define a new function, ask-1, to get answers one at a time, and
- redefine ask to get all the answers that ask-1 can generate.
The new ask should still pass all the tests in ddr-tests.lisp.
The syntax of ask-1 is like ask. I.e.,
- DDR: (ask-1 [query [ form ]])
- SDDR: (ask-1 [query rules])
Note that query is optional in both cases. The semantics of ask-1 is:
- if a query is given, return the first answer, if any
- if query is not given, return the next answer for whatever query was previously given
Here's an example of how ask-1 should work in DDR with one of the test knowledge bases in ddr-tests.lisp:
DDR-TESTS 16 > (make-tiger-kb) ... DDR-TESTS 17 > (ask '(can-satisfy-hunger ?x)) ((CAN-SATISFY-HUNGER ANTELOPE) (CAN-SATISFY-HUNGER TIGER)) DDR-TESTS 18 > (ask-1 '(can-satisfy-hunger ?x)) (CAN-SATISFY-HUNGER ANTELOPE) DDR-TESTS 19 > (ask-1) (CAN-SATISFY-HUNGER TIGER) DDR-TESTS 20 > (ask-1) NIL
As with ask in DDR, if form is omitted, it should default to query. In SDDR, both the original query and rule base should be remembered. If (ask-1) is evaluated and no previous query has been specified, (ask-1) should return false.
Approach
This problem has both a conceptual challenge and a software programming challenge. The conceptual challenge is how to represent the state of the deductive search in a way that supports getting answers one at a time. The programming challenge is how to make as few changes as possible to the existing tested retriever code.
The current code uses a simple uniform recursive logic: explore all branches and append all results. This automatically takes care of branches that lead to no results or many. But it means that the code has many functions calling other functions recursively, expecting to get lists of all answers back. If now only one answer is returned, how can the basic logic structure be kept?
The answer is generated lists, also known as lazy lists and, in Abelson and Sussman's Structure and Interpretation of Computer Programs, streams. A generated list is a data structure with list-like operations, analogous to car and cdr, but the elements of a generated list may not exist until accessed. That is, the elements may be generate on demand.
The glist package defines some basic functions that create and manipulate generated lists. Most of these functions are analogous to the standard list functions: gcar, gcdr, gappend and so on.
Because generated list functions work much like regular list functions, converting code using lists to generated lists is much less work than completely redoing the logic of the retriever to keep a queue of answers. Instead of consing or appending lists of all answers, you gcons or gappend them.
Be careful. Do not just generate all the answers and then store
the results in a generated list. Only the work needed to find one solution
should happen for the first call to ask-1.
The work to find the next solution should only happen if
you call ask-1 again. You need to look inside the code
for where backchaining occurs, both in
the main code
and some of the logic extensions, like and and not.
Do not convert all lists to lazy lists. Only lists that involve recursively finding alternative solutions should be converted. Other lists, e.g., the list of bindings returned by unification, should remain normal lists.
Hint: you may find it useful to first convert some code
using loops, e,g., loop ... append ... to a
recursive form first. Change and test first, then
introduce generated lists.
You'll need a few top-level global variables to hold the inputs and generated list of answers. ask-1 should set these variables when a new query is passed in. ask-1 should then pop off the next answer from the generated list. ask simply calls ask-1 repeatedly until it returns false, and collects all the answers.
Exercise: DDR Deductive JavaScript
Under construction
Port the simple deductive retriever to JavaScript.
The key subtasks are:
- Representing backward chaining rules
- Implementing the unifier algorithm
- Implementing the backward chaining algorithm
Representing backward chaining rules
In Lisp, a rule is a simple list, such as
(<- (can-move ?x) (block ?x) (clear ?x))
This is why Lisp works so well for AI. We didn't have to do anything to implement an external rule syntax.
In JavaScript we have some choices to make and work to do. We could map the Lisp list form to arrays like this:
["<-", ["canMove", "?x"], ["isBlock", "?x"], ["isClear", "?x"]]
This is pretty hard to read, and the code to matching and inference will be littered with cryptic array indices.
A JavaScript object approach might be like this:
{
"consequent": { "canMove": ["?x"] },
"antecedents": [ { "isBlock": ["?x"] }, { "isClear": ["?x"] }]
}
We could include functional terms using nested objects. For example here's one of the deductive rules for append in object form:
{
"consequent": { "append": [{ "cons", [?x, "?l1"] }, "?l2", { "cons", [?x, "?l3"] }] },
"antecedents": [ { "append": ["?l1", "?l2", "?l3"] }]
}
Code to match and infer with this format will be pretty clear, with references to rule.consequent and rule.antecedents, rather than array indices.
We'll use this for now. One of the exercises below will use fluent programming to make it easier to write rule objects.
Unification
Implement unify(form1, form2, [binding-lists]).
As with
the JavaScript matcher,
unify should take an optional list of binding lists.
Each binding list is an object with variables as keys and binding value as the values
of those keys, e.g.,
{ "?x": "a", "?y": "b" }. The default value for the third argument
to unify is the list of the empty object. unify should return
a (possibly empty) list of the binding lists that unify the two forms.
Forms to be matched can be:
- variables, i.e., strings beginning with a question mark
- primitives, i.e., strings, numbers, null
- arrays of forms, such as argument lists, and
- objects, such as
{ "isBlock": ["block1"] }.
You have to handle variables on both sides and appropriately deal with circular bindings. Use the same logic as the Lisp code.
Warning: var is a reserved word in JavaScript. You will get syntax errors if you try to use it as a variable name.
Backward chaining
Implement ask(assertion). The primary subfunctions will be as in the Lisp code:
- prove(assertion binding-lists) to do the actual backward chaining, looping over rules and binding lists
- renameVariables(rule) to avoid variable name collision
- instantiate(form binding-list) to make an instance of a form given a binding list
For renameVariables(), you need to define a variable generator function, equivalent to gentemp in Lisp, that you can call as needed to get a guaranteed new variables on each call, such as "?1012", "?1013", ...
Fluent rule construction
Define a function If() for building rules in a fluent programming style. The capitalization is important to avoid conflict with the Javascript reserved word if. For example, to do the "can move" rule,
{
"consequent": { "canMove": ["?x"] },
"antecedents": [ { "isBlock": ["?x"] }, { "isClear": ["?x"] }]
}
you would write
If("isBlock", "?x").and("isClear", "?x").then("canMove", "?x")
You could set the variable appendKb to a list of the two "append" inference rules by writing with
const appendKb = [
If().then("append", null, "?l", "?l"),
If("append", "?l1", "?l2", "?l3").then("append", {"cons": ["?x", "?l1"] }, "?l2", { "cons": ["?x", "?l3"] })
]
rather than
const appendKb = [{
"consequent": { "append": [null, "?l", "?l"] }
}, {
"consequent": { "append": [{ "cons": ["?x", "?l1"] }, "?l2", { "cons": ["?x", "?l3"] }] },
"antecedents": [ { "append": ["?l1", "?l2", "?l3"] }]
}]
Fluent programming involves calling a function that creates a fluent object. A fluent object has internal data, and one or more methods to modify that data. Most of the fluent object methods return the object, so that methods can be chained together. At least one method is a terminating method that returns the internal data as a regular JavaScript object.
In this case, If(predicate, ...args) should create an initial fluent object. The given predicate and arguments should be stored internally, as the first in a list of antecedents. The fluent object has two methods:
- and(predicate, ...args) adds another predicate and arguments to the antecedents list, and returns the fluent object.
- then(predicate, ...args) terminates the chain and returns a non-fluent Javascript inference rule object with the antecedents collect, and the given predicate and arguments as the consequent.
A call to If() with no arguments should start a rule with an empty antecedent list.
If(), and(), and then() all need to take a rest parameter to get the arguments for a predicate. You'll also need to understand how closures work. It's the same in JavaScript as in Lisp.