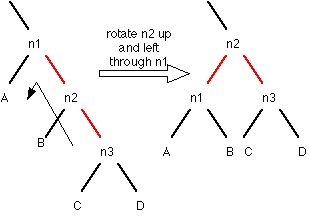
Note that the parent link colors of n1 and n2 have flipped.
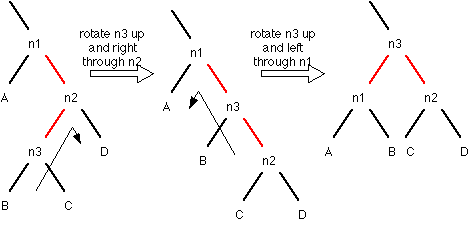
Note that the second rotation here is exactly the same as in the previous case. n1 and n3 flip their parent link colors.
| EECS 311: Red-Black Trees |
Home Course Info Links Grades |
Lectures Newsgroup Homework Exams |
Red-black trees are binary search trees. Like AVL trees, we keep a little extra bookkeeping information on each node, but very little -- just one bit, in fact. If this bit is on, we say that the node has a red link to its parent. If it's off, the node has a black link to its parent.
Maintaining a red-black tree as new nodes are added primarily involves recoloring and rotation, as follows:
There are four cases where rotations have to occur:

Note that the parent link colors of n1 and n2 have flipped.

Note that the second rotation here is exactly the same as in the previous case. n1 and n3 flip their parent link colors.
There are 3 things you have to verify about this and any algorithm:
The first two can be handled inductively, by showing that every step preserves the properties of binary search trees. Therefore, if the tree starts correctly, it will stay correct.
An upper bound on the complexity can be found by noting two invariant properties that the above algorithm maintains:
From these two properties, it follows that the paths are always O(log n) long.
There's an interactive Java animation that shows the operation of red-black trees at http://reptar.uta.edu/NOTES5311/REDBLACK/RedBlack.html. Note that:
A good way to understand how red-black trees work is to play with this simulation until you can always correctly predict what it's going to do when you hit the "Next" button.
Implementation of red-black trees for insertion is mostly a matter of carefully handling all the rotations. If your tree nodes do not have links to their parents, then, while your code descends the tree, it needs to pass along as parameters the most recent 4 nodes in the path from root to leaf, i.e., a node, its parent, its grandparent, and its great-grandparent.
Deletion is more complex, though still O(log N).
Comments?  Send mail to
c-riesbeck@northwestern.edu.
Send mail to
c-riesbeck@northwestern.edu.